[/_header.htm]

Wulfenite

THE TETRAGONAL
CRYSTAL SYSTEM

class name, number, symmetry
Ditetragonal Dipyramidal Class, 27th, 4/m 2/m 2/m

Tetragonal Trapezohedral Class, 26th, 4 2 2

Ditetragonal Pyramidal Class, 25th, 4 m m

Tetragonal Scalahedral Class, 24th, bar 4 2 m

Tetragonal Dipyramidal Class, 23rd, 4/m

Tetragonal Disphenoidal Class, 22nd, bar 4

Tetragonal Pyramidal Class, 21st, 4

[/_inline.htm]

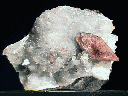
SOME TETRAGONAL
MINERALS

ZIRCON

CARLETONITE

RUTILE

SCAPOLITE

ANATASE

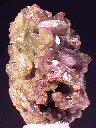
VESUVIANITE

NARSARSUKITE

AUTUNITE

XENOTIME

THORITE

ZEUNERITE

The tetragonal system is the least populated by natural crystals of all the crystallographic systems. The basic setup is similar to the isometric system in that all angles between the crystallographic axes are 90 degrees. The difference between the isometric system and the tetragonal system is that one of the three axes is longer or shorter than the other two. This produces a unique direction in the tetragonal crystals giving rise to the reference of the tetragonal system as uniaxial. This unique direction in the crystal becomes the major axis, also called the c axis. The other two axes are identical and are referred to as a and a'.

The basic form of the isometric system can be thought of as a square box; however, in the tetragonal system the basic form can be thought of as either an elongated or a flattened box. The box will still have a square cross-section, but side profiles will show rectangles. The direction through the square cross-section defines the four fold rotational axis, or the c axis, that is required for this system. Tetragonal crystals that have a box like form or a pyramidal form can be pseudo- cubic or pseudo- octahedral, respectively. This occurs if the major axis is similar in length to the other axes or if the crystal simply did not grow fast enough or slow enough, which ever the case may be, in the major axis direction.

The system's most symmetrical class, the Ditetragonal Dipyramidal Class, has a mirror plane perpendicular to the major axis. Each of the two identical crystallographic axes (a and a') serve as the 2 two fold rotational axes. Two mirror planes are also found running parallel to the major axis and are perpendicular to the two fold axes. With all this symmetry, more symmetry is actually produced from the position of the mirrors and axes. Two more two fold axes are found between the a and a' axes in the plane perpendicular to the major axis. Also two more mirror planes are found parallel to the major axis, again between the other two mirror planes. The four separate mirrors divide the crystal into 45 degree slices just as four cuts through a pizza divide it into eight slices. The eight slices are an analogous representation of the ditetragonal (or 2 X 4 sided) aspect of this class and the Ditetragonal Pyramidal Class which lacks the perpendicular mirror and the two fold axes.

The other lower symmetry classes have few minerals as members and fewer minerals that crystallize well enough to show their true symmetry. The Tetragonal Scalahedron Class and the Tetragonal Disphenoidal Class do not even appear to belong to the tetragonal system as they seem to lack a four fold axis. They don't really lack a four fold axis, it's just a four fold rotoinversion axis. A tetragonal rotoinversion axis takes a face, rotates it 90 degrees (one fourth of a rotation) and then inverts it (up to down & right to left) through the crystal to the other side. Then it rotates it again 90 degrees and inverts it again through the crystal. Another rotoinversion operation and finally another (four in all) and it is back exactly where it started. The result is two major faces on the top and two on the bottom of the crystal but in perpendicular orientation. The axis then looks like a two fold axis instead of the four fold axis that it actually is. The tetragonal scalahedron has eight faces (four pairs) instead of the four faces of the tetragonal diphenoid, but the symmetry operation is the same.

The other classes include the Tetragonal Trapezohedral Class which lacks any mirror planes and is analogous to other trapezohedral classes of other systems such as the Trigonal Trapezohedral Class, 12th, (3 2) and the Hexagonal Trapezohedral Class, 19th, (6 2 2).

The Tetragonal Dipyramidal Class and the Tetragonal Pyramidal Class simply have a four fold axis with no parallel mirrors or any two fold axes. The difference between these last two classes is the presence, or lack there of, of a perpendicular mirror plane. A dipyramid is just a pyramid on top that is then reflected on the bottom.

Ditetragonal Dipyramidal Class

Apophyllite

Class: 27th
Symmetry: 4/m 2/m 2/m
Symmetry Elements: There is 1 four fold axis, 4 two fold axes, 5 mirror planes each perpendicular to one of the rotational axes and a center.
Crystallographic Axes: Two axes, a and a' are equal to each other, but they are either shorter or longer than the c axis.
Angles: All three angles = 90 degrees.
Common Forms: The ditetragonal dipyramid, tetragonal dipyramid, ditetragonal prism, tetragonal prism and the basal pinacoid.
Most Common Minerals Know to this Class: Apophyllite, autunite, meta-autunite, torbernite, meta-torbernite, xenotime, carletonite, plattnerite, zircon, hausmannite, pyrolusite, thorite, anatase, vesuvianite, rutile and cassiterite as well as meta-ankoleite, calomel, phosgenite, thorogummite, uranospinite, pseudoboleite, cumengite, uranocircite, melanophlogite, zeunerite and stishovite among many other rarer minerals.

Tetragonal Trapezohedral Class

Wardite

Class: 26th
Symmetry: 4 2 2
Symmetry Elements: There is 1 four fold axis and 2 two fold axes, all are perpendicular to the other rotational axes.
Crystallographic Axes: Two axes, a and a' are equal to each other, but they are either shorter or longer than the c axis.
Angles: All three angles = 90 degrees.
Of Note: The crystals can be either left or right handed, enantiomorphic.
Common Forms: The tetragonal trapezohedron, ditetragonal prism, tetragonal prism, tetragonal dipyramid and the basal pinacoid.
Most Common Minerals Know to this Class: Wardite and cristobalite are the only somewhat common members of this class, but some other members include: maucherite, mellite, genkinite, vinciennite, ekanite and formicaite.

Ditetragonal Pyramidal Class

Class: 25th
Symmetry: 4 m m
Symmetry Elements: There is 1 four fold axis and 4 mirror planes.
Crystallographic Axes: Two axes, a and a' are equal to each other, but they are either shorter or longer than the c axis.
Angles: All three angles = 90 degrees.
Of Note: Crystals of this group are hemimorphic, ie. different top and bottom.
Common Forms: The ditetragonal pyramid, ditetragonal prism, tetragonal prism, tetragonal pyramid and the pedion (note: not the pinacoid).
Most Common Minerals Know to this Class: Diaboleite, diomignite, fresnoite, hematophanite and routhierite are the only known minerals that belongs to this class.

Tetragonal Scalahedron Class

Chalcopyrite

Class number: 24th
Symmetry: Bar 4 2 m
Symmetry Elements: There is 1 four fold rotoinversion axis (appears as a two fold axis), 2 two fold axes and 2 mirror planes.
Crystallographic Axes: Two axes, a and a' are equal to each other, but they are either shorter or longer than the c axis.
Angles: All three angles = 90 degrees.
Of note: Crystals of this class form wedge shaped crystals that look like orthorhombic crystals.
Common Forms:The tetragonal scalahedron, disphenoid, ditetragonal prism, tetragonal prism, tetragonal dipyramid and pinacoid.
Most Common Minerals Know to this Class: Chalcopyrite and stannite as well as akermanite, hardystonite, melilite, urea, luzonite, pirquitasite, renierite and tetranatrolite.

Tetragonal Dipyramidal Class

Scheelite

Class: 23rd
Symmetry: 4/m
Symmetry Elements: There is 1 four fold axis and a mirror plane that is perpendicular to the rotational axis.
Crystallographic Axes: Two axes, a and a' are equal to each other, but they are either shorter or longer than the c axis.
Angles: All three angles = 90 degrees.
Common Forms: The tetragonal dipyramid, tetragonal prism and the pinacoid.
Most Common Minerals Know to this Class: Scapolite, wulfenite, vesuvianite, powellite, narsarsukite, meta-zeunerite, leucite, fergusonite and scheelite.

Tetragonal Disphenoidal Class

Class: 22nd
Symmetry: Bar 4
Symmetry Elements: There is only 1 four fold rotoinversion axis (appears as a two fold axis).
Crystallographic Axes: Two axes, a and a' are equal to each other, but they are either shorter or longer than the c axis.
Angles: All three angles = 90 degrees.
Common Forms: The tetragonal disphenoidal, tetragonal prism and the pinacoid.
Of note: Crystals of this class form wedge shaped crystals that look like orthorhombic crystals.
Most Common Minerals Know to this Class: Cahnite, minium, nagyagite, tugtupite and some rather rare minerals such as crookesite, meliphanite, schreibersite and vincentite.

Tetragonal Pyramidal Class

Wulfenite ???

Class: 21st
Symmetry: 4
Symmetry Elements: There is only 1 four fold axis.
Crystallographic Axes: Two axes, a and a' are equal to each other, but they are either shorter or longer than the c axis.
Angles: All three angles = 90 degrees.
Of Note: Crystals of this group are hemimorphic, ie. different top and bottom.
Common Forms:The tetragonal pyramid, tetragonal prism and pedion (note: not the pinacoid).
Most Common Minerals Known of this Class: Wulfenite is believed to belong to this class, but this is in dispute as it may belong to the Tetragonal Dipyramidal class. Other members of this class are rare and include; Pinnoite, piypite, richellite and stenhuggarite.

THE TETRAGONAL CRYSTAL SYSTEM